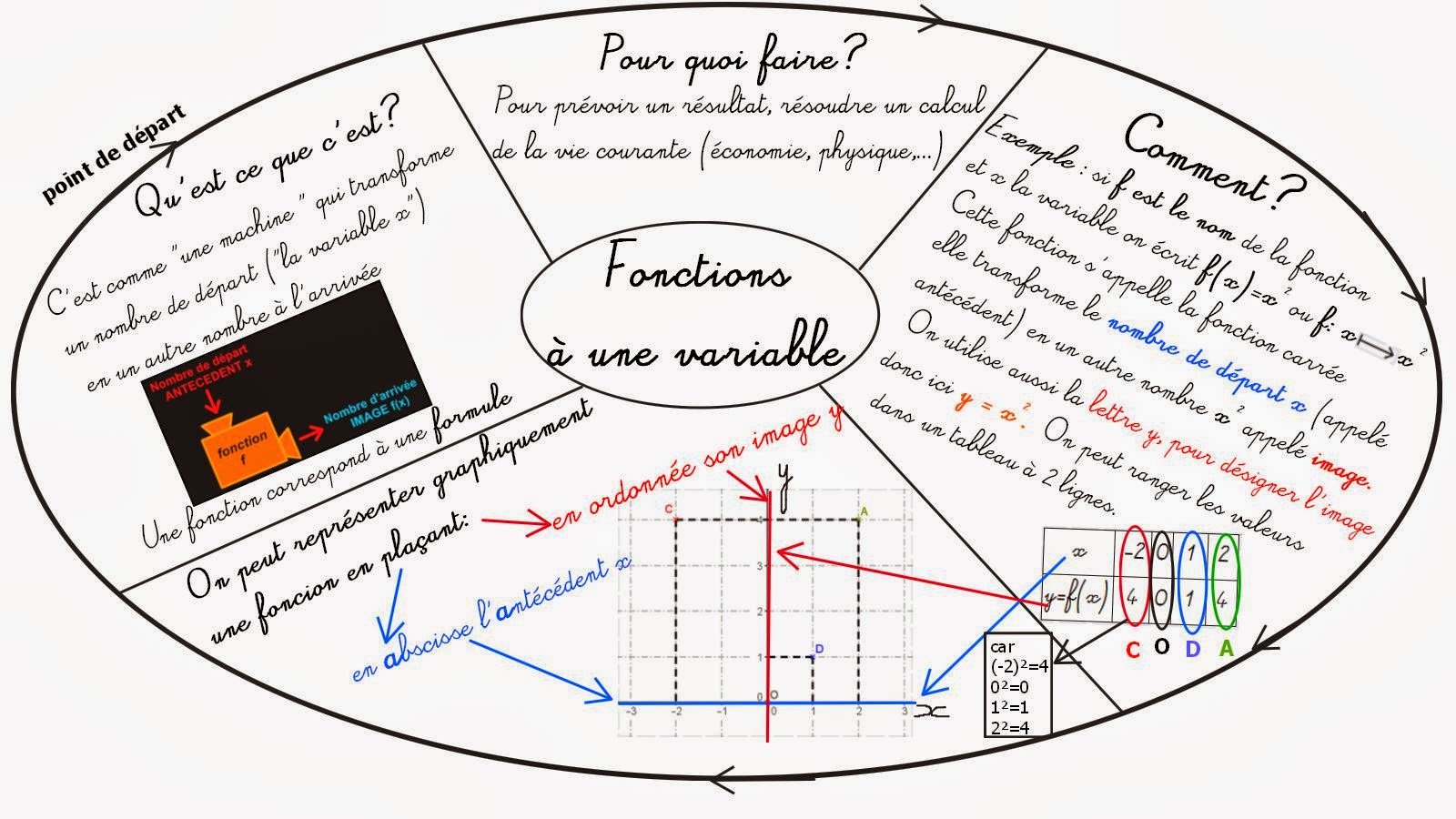
Carte mentale Calcul Littéral version élève incomplète Les "branches" de cette carte mentale sont à colorier. Dans "C'est quoi": c'est un calcul comportant des nombres inconnus qui sont remplacés par des lettres Dans "Pourquoi?": le calcul littéral est utilisé dans des formules en géométrie (aires, périmètres, volumes), mais aussi en physique, etc... Développer c'est transformer un produit en une somme (on "vide" les 4 trousses qui symbolisent les parenthèses) Suppression de parenthèse: lorsque la parenthèse est précédée d'un "+" on peut enlever les parenthèses sans rien changer lorsque la parenthèse est précédée d'un "-" on peut enlever les parenthèses mais les termes se trouvant dans la parenthèse se transforment en leur opposé Factoriser c'est transformer une somme en un produit NOUVEAU: Vidéo explicative + version complète